COMPUTATION OF AREA AND VOLUME

 

COMPUTATION OF AREA AND VOLUME

 

AREAS

The method of computation of area depends upon the shape of the boundary of the tract and accuracy required. The area of the tract of the land is computed from its plan which may be enclosed by straight, irregular or combination of straight and irregular boundaries. When the boundaries

are straight the area is determined by subdividing the plan into simple geometrical figures such as triangles, rectangles, trapezoids, etc. For irregular boundaries, they are replaced by short straight boundaries, and the area is computed using approximate methods or Planimeter when the boundaries are very irregular. Standard expressions as given below are available for the areas of straight figures.

 

Area of triangle = ½absinθ

 Where   θ is the included angle between the sides a and b.

                          Or       

Area of triangle = √{s(s-a)(s-b)(s-c)}

 Where   a, b and c are the sides,

 And         s = ½(a+b+c)

                       Or

Area of triangle = ½ x b x h

 Where   b = base and h = altitude.

 Area of a rectangle = a x b

 Where    a and b are the sides.

 Area of trapezium = ½ x (a+b) x h

 Where  a and b are the parallel sides separated by perpendicular distance h.

 Various methods of determining area are discussed below.

Area Enclosed by Irregular Boundaries

 Two fundamental rules exist for the determination of areas of irregular figures as shown in Fig A.1. These rules are (i) Trapezoidal rule and (ii) Simpson's rule.

Trapezoidal Rule

In trapezoidal rule, the area is divided into a number of trapezoids, boundaries being assumed to be straight between pairs of offsets. The area of each trapezoid is determined and added together to derive the whole area. If there are n offsets at equal interval of d then the total area is

 

A = d( O₁+On + O₂+ O₃ + ......... + On-₁)

              2

 While using the trapezoidal rule, the end ordinates must be considered even they happen to be zero.

 

Simpson's Rule

In Simpson's rule it is assumed that the irregular boundary is made up of parabolic arcs. The areas of the successive pairs of intercepts are added together to get the total area.

A = d[(O₁+On) + 4(O₂+O₄+.......+ On-₂) + 2(O₃+O₅+....... + On-₁)]

       3

   = Common Distance[(1^st Ordinate+Last Ordinate)+4(Sum of Even Ordinate)

                  3

                            +2(Sum of Odd Ordinates)]

 

Since pairs of intercepts are taken, it will be evident that the number of intercepts n is even. If n is odd then the first or last intercept is treated as a trapezoid.

 

Coordinate Method of Finding Area.

 When the offsets are taken at very irregular intervals, then the application of the trapezoidal rule and Simpson’s rule is very difficult. In such a case, the coordinate method is appropriate.

Procedure

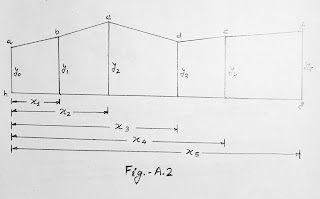
From the given distances and offsets, appoint is selected as the origin in Fig A.2.

Taking h as the origin, the coordinates of all other points are arranged as follows.

 

Points	Coordinates
	X	Y
a	0	y₀
b	x₁	y₁
c	x₂	y₂
d	x₃	y₃
e	x₄	y₄
f	x₅	y₅
g	x₅	0
h	0	0
a	0	y₀

 

The coordinates are arranged in determinant form as follows.

 

Sum of products along the solid line,

 ∑P = (y₀x₁ + y₁x₂ + y₂x₃ + y₃x₄ + y₄x₅ + y₅x₅ + 0.0 + 0.0)

 Sum of products along the dotted line,

 ∑Q = (0.y₁ + x₁y₂ + x₂y₃ + x₃y₄ + x₄y₅ + x₅.0 + x₅.0 + y₀.0)

 Required area = ½(∑P-∑Q)

 

Planimeter

An integrating device, the planimeter, is used for the direct measurement of area of all shapes, regular or irregular, with a high degree of accuracy.

The area of plan is calculated from the following formula when using Amsler polar planimeter.

A = M(R₂ - R₁ ±10N + C)

 Where  

M = the multiplying constant of the instrument. Its value is marked on the   tracing arm of the instrument,

 R₁ and R₂ = the initial and final readings,

 N = the number of complete revolutions of the dial taken positive when the zero mark passes the index mark in a clockwise direction and 'negative’ when in counterclockwise direction, and

 C = the constant of the instrument marked on the instrument arm just above the scale divisions. Its value is taken as zero when the needle point is kept outside the area. For the needle point inside, -the value of MC is equal to the area of zero circle.

 

(Next post on “COMPUTATION OF VOLUME”)